Finding the Integral of a Product of Two Functions

Sometimes the function that you’re trying to integrate is the product of two functions — for example, sin³x and cos x. This would be simple to differentiate with the Product Rule, but integration doesn’t have a Product Rule. Fortunately, variable substitution comes to the rescue.

Given the example,

follow these steps:

1. Declare a variable as follows and substitute it into the integral:

   Let u = sin x

   You can substitute this variable into the expression that you want to integrate as follows:

   

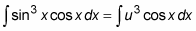
   Notice that the expression cos x dx still remains and needs to be expressed in terms of u.

2. Differentiate the function u = sin x.

   This gives you the differential du = cos x dx.

3. Substitute du for cos x dx in the integral:

   

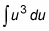
4. Now you have an expression that you can integrate:

   

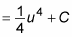
5. Substitute sin x for u:

   

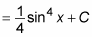
Now check this answer by differentiating with the Chain Rule:

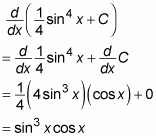
This derivative matches the original function, so the integration is correct.