You can distinguish among linear, separable, and exact differential equations if you know what to look for. Keep in mind that you may need to reshuffle an equation to identify it.
Linear differential equations involve only derivatives of y and terms of y to the first power, not raised to any higher power. (Note: This is the power the derivative is raised to, not the order of the derivative.) For example, this is a linear differential equation because it contains only derivatives raised to the first power:
Separable differential equations can be written so that all terms in x and all terms in y appear on opposite sides of the equation. Here's an example:
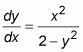
which can be written like this with a little reshuffling:
Exact differential equations are those where you can find a function whose partial derivatives correspond to the terms in a given differential equation.





