In many games, one player chooses before another, and it’s difficult to know who has the advantage. In macro-economic models of business situations, if you move first, your rival may be able to neutralize your decision by moving second. You need to develop a decision-making rule that helps you anticipate your rival’s decision.
Decision-makers use backward induction in sequential games. Backward induction means that you develop your decision by looking at the future, or at how the game ends. Consider the decision tree in the illustration. Two car dealers, Cathy’s Cars and Otto’s Autos, must decide whether to raise, lower, or charge the same price on their used cars.
Because of her leadership position in the market, Cathy’s Cars chooses her used car price first, and then Otto’s Autos follows. When establishing her price, Cathy needs to consider how Otto responds by using backward induction. Using backward induction requires the following steps. Decision-makers start at the end of the game.
The player making the last decision chooses the decision that has the greatest payoff. As a result, the player making a decision in the step before the last decision takes into account the likely decision in the last step when making her decision.
Decision-makers continue working backward from the last decision, taking into account the likely decision made at each step in the sequence, until the first step — the initial decision step — is reached. The illustration shows the backward induction process.
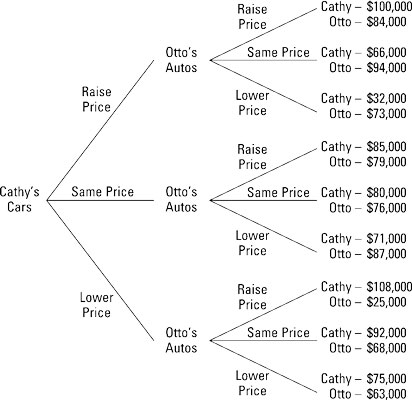
The illustration summarizes the various outcomes that are possible in the situation. The far left starts with Cathy’s possible choices — she can raise price, charge the same price, or lower price. In the middle, Otto’s choices are portrayed for each possible choice Cathy can make. At the far right are the annual profits each dealer receives given their combined choices.
For example, if Cathy lowers price, follow the lower branch from Cathy’s Cars to Otto’s Autos. If Otto charges the same price, follow the middle branch to the outcome — $92,000 profit for Cathy and $68,000 profit for Otto. Thus, when making her decision, Cathy needs to consider how Otto responds.
If Cathy raises price, Otto charges the same price to earn $94,000.
Otto charges the same price because $94,000 is a higher profit for Otto than $84,000 if he raises price or $73,000 if he lowers price. As a result, Cathy’s profit is $66,000.
If Cathy charges the same price, Otto lowers price to earn $87,000.
Otto lowers price because $87,000 is a higher profit than $79,000 if Otto raises price or $76,000 if he charges the same price. Cathy’s profit is $71,000 — the result of her charging the same price and Otto lowering price.
If Cathy lowers price, Otto charges the same price to earn $68,000.
Otto charges the same price because $68,000 is a higher profit than $25,000 if Otto raises price or $63,000 if he lowers price. Cathy’s profit is $92,000.
Cathy’s decision is to lower price.
When Cathy lowers her price, Otto charges the same price, resulting in $92,000 profit for Cathy and $68,000 profit for Otto. The $92,000 profit for Cathy is the best she can expect after Otto makes his choice. As indicated in Step 1, if Cathy raises price she ultimately receives $66,000 in profit and if she charges the same price, she receives $71,000 in profit as indicated in Step 2.
By using backward induction to anticipate Otto’s response to her decision, Cathy is able to choose the best possible action.

