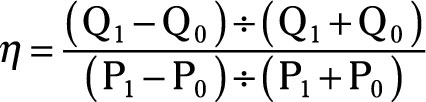Price elasticity of demand formula
The formula used to calculate the price elasticity of demand is:The symbol η represents the price elasticity of demand. The symbol Q0 represents the initial quantity demanded that exists when the price equals P0. The symbol Q1 represents the new quantity demanded that exists when the price changes to P1.
In this formula, the price elasticity of demand will always be a negative number because of the inverse relationship between price and quantity demanded. As price went up, quantity demanded went down, or vice versa. When price goes down, quantity demanded goes up. Price and quantity demanded always move in opposite directions, hence the price elasticity of demand is always negative.
How to find price elasticity of demand: example problem
Suppose that you own a company that supplies vending machines. Currently, your vending machines sell soft drinks at $1.50 per bottle. At that price, customers purchase 2,000 bottles per week. In order to increase sales, you decide to decrease the price to $1, and sales increase to 4,000 bottles.To calculate the price elasticity of demand, here’s what you do:
-
Plug in the values for each symbol.
Because $1.50 and 2,000 are the initial price and quantity, put $1.50 into P0 and 2,000 into Q0. And because $1.00 and 4,000 are the new price and quantity, put $1.00 into P1 and 4,000 into Q1.
-
Work out the expression on the top of the formula.
Start by dividing the expression on top of the equation. (Q1 – Q0) equals 2,000, and (Q1 + Q0) equals 6,000. Dividing 2,000 by 6,000 equals 1/3.
-
Work out the expression in the bottom of the equation.
(P1 – P0) equals –$0.50, and (P1 + P0) equals $2.50. Dividing –$0.50 by $2.50 equals –1/5.
-
Do the final division of the remaining values on the top and bottom of the equation.
Divide the top result, 1/3, by the bottom result, –1/5, to get the price elasticity of demand of –5/3 (or –1.67).
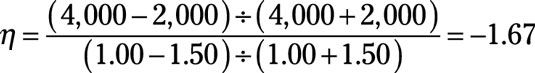
The price elasticity of demand is simply a number; it is not a monetary value. What the number tells you is a 1 percent decrease in price causes a 1.67 percent increase in quantity demanded. In other words, quantity demanded’s percentage increase is greater than the percentage decrease in price.
Thus, when you decrease the price of soft drinks, you will sell a lot more soft drinks, and your revenue will go up (from $3,000 to $4,000).
Whenever the absolute value of demand is greater than one, price decreases will increase revenue.