The regression function is usually expressed mathematically in one of the following ways: basic notation, summation notation, or matrix notation. The Y variable represents the outcome you’re interested in, called the dependent variable, and the Xs represent all the independent (or explanatory) variables. Your objective now is to estimate the population regression function (PRF) using your sample data.
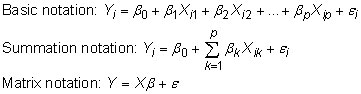
When working on real-world econometric problems, you usually specify a PRF with a dependent variable and several independent variables. For example, suppose you’re interested in the number of hamburgers purchased during the lunch hour at school cafeterias.
Microeconomic theory suggests that sales should be influenced by the price of the hamburgers along with other factors, such as the price of other food items, the price of soft drinks, and so on. With that in mind, you may want to specify your PRF using hamburger sales as the dependent variable and all other relevant factors as the independent variables.
To visualize the OLS regression and get a basic understanding of the fundamental concept, assume now that the dependent variable (hamburger sales) is influenced by only one explanatory variable (the price of hamburgers).
The sample regression function (SRF) is expressed as
where Y is hamburger sales and X is the price. In this case, the SRF is a line, with the value for
estimating the intercept and
estimating the value of the slope.
Notice how the mathematical representation of the SRF uses hats (^) above the coefficients and error term. This symbol is used to denote that these numbers are estimates of their true population values, but keep in mind that some textbooks use English (Latin) letters to represent sample regression coefficients and other estimates.

