When you need to estimate a sample regression function (SRF), the most common econometric method is the ordinary least squares (OLS) technique, which uses the least squares principle to fit a prespecified regression function through your sample data.
The least squares principle states that the SRF should be constructed (with the constant and slope values) so that the sum of the squared distance between the observed values of your dependent variable and the values estimated from your SRF is minimized (the smallest possible value).
Although sometimes alternative methods to OLS are necessary, in most situations, OLS remains the most popular technique for estimating regressions for the following three reasons:
Using OLS is easier than the alternatives. Other techniques, including generalized method of moments (GMM) and maximum likelihood (ML) estimation, can be used to estimate regression functions, but they require more mathematical sophistication and more computing power. These days you’ll probably always have all the computing power you need, but historically it did limit the popularity of other techniques relative to OLS.
OLS is sensible. By using squared residuals, you can avoid positive and negative residuals canceling each other out and find a regression line that’s as close as possible to the observed data points.
OLS results have desirable characteristics. A desirable attribute of any estimator is for it to be a good predictor. When you use OLS, the following helpful numerical properties are associated with the results:
The regression line always passes through the sample means of Y and X or
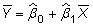
The mean of the estimated (predicted) Y value is equal to the mean value of the actual Y or
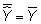
The mean of the residuals is zero, or
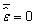
The residuals are uncorrelated with the predicted Y, or
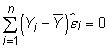
The residuals are uncorrelated with observed values of the independent variable, or
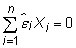
The OLS properties are used for various proofs in econometrics, but they also illustrate that your predictions will be perfect, on average. This conclusion follows from the regression line passing through the sample means, the mean of your predictions equaling the mean of your data values, and from the fact that your average residual will be zero.

