In Common Core math, your child uses math symbols to solve problems, and so she needs to have some understanding about how to use them. This is where order of operations becomes important.
The order of operations, or the sequence to follow when calculating the result of using different operations, is particularly significant for fifth graders.
Your child may use the mnemonic device Please Excuse My Dear Aunt Sally, abbreviated frequently as PEMDAS. Someone thought up this little tool long ago to help students remember the order of operations. PEMDAS stands for the following, which you do in this order:
Parentheses: Do any of the computations inside of parentheses first (and follow the order of operations within those parentheses, if there is more than one operation inside them).
Exponents: Calculate the results of any exponents or radicals (such as square roots).
Multiplication and division: Do any multiplication and division next. These two operations come in the same step together, not one before the other.
Addition and subtraction: Like with multiplication and division, do these operations in the same step.
Within each of these four steps, you go from left‐to‐right. So 8 – 4 + 1 is 5, not 3. (You get 3 by adding 4 and 1 first then subtracting the result from 8.) In fact, a simple expression such as 8 – 4 + 1 points out the need for an order of operations. It would be a disaster if people couldn't agree on the value of such a simple expression.
As an example of the disasters that can occur when an expression is written poorly, you can easily find arguments about this expression on social media:
Following the strict PEMDAS interpretation, you would calculate the value of this expression like this:
Add 9 and 3, leaving
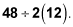
Divide 48 by 2, leaving 24(12).
Multiply 24(12), getting 288.
But PEMDAS misses some subtleties. Among these subtleties are the following rules, which are often unspoken:
Do implied multiplications before division or explicit multiplication. Implied multiplication refers to something such as the 2(12) seen in the above expression, where there is no multiplication symbol.
Factorials come before exponents. A factorial is a number with an exclamation point after it (like this: 3!); they are useful in a number of areas in math, especially probability. The expression "3!" doesn't mean someone is exclaiming the number three; it means to multiply 3 by all the smaller whole numbers, ending with 1. So 4! means
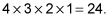
PEMDAS doesn't have an F (for factorial), so mathematicians have agreed that factorials come between parentheses and exponents in the order of operations, but this part of the rule usually isn't taught in school.
Calculate exponents within exponents from right to left. An expression such as
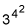
should be evaluated from the rightmost (or highest) exponent to the left (or down). So
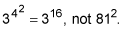
(The difference between these two expressions is more than 43 million.)
The expression
trips up people who pay attention to the unspoken rule about implied multiplication. These people will calculate the expression this way:
Add 9 and 3, leaving
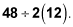
Multiply 2 by 12, leaving
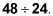
Divide, getting 2.
Or maybe it doesn't trip these people. Maybe these people got it right. There is really no way to know what the person who wrote the expression meant for it to say, and that brings you back to where you started.
The order of operations is an agreement among people that eases communication. If someone writes an ambiguous expression, such as
then shame on that person for writing an ambiguous expression. If that person meant
then that's what he should have written. If he meant
then he should have written that. The order of operations doesn't exist to trick people with ambiguous mathematical expressions; it exists so that people can communicate their ideas more effectively.

